Right off the bat, I will start this blog by starting a series on a gentle introduction to my favorite topic: matroids.

The first time I heard about matroids was actually after I got my Master’s degree when I was still employed as a TA at the Theoretical Computer Science group at RWTH Aachen. A few months later when I joined the Chair of Management Science as PhD student, they somehow became a main part of what I was working on. A matroid is a neat structure defined on a finite ground set $E$. Usually one is interested in a question like

“Which elements from $E$ can I pick such that my collection is not in some way constricted?”

Sometimes this kind of question depends simply on the number of elements that I pick, i.e. as long as i do not pick too many elements, my collection is feasible. In other cases, the cardinality of my set is less important, but I have that there are not two (or more) elements included that can not go along with each other.

One of the easiest example for matroids are undirected graphs, which I will denote by $G = (V, E)$. The set $V$ contains the vertices of the graph, while $E \subseteq \{e \subseteq V \mid |e| \in \{1, 2\}\}$ contains the edges, i.e. the connections between vertices. A graph can be pictured as in the figure below.

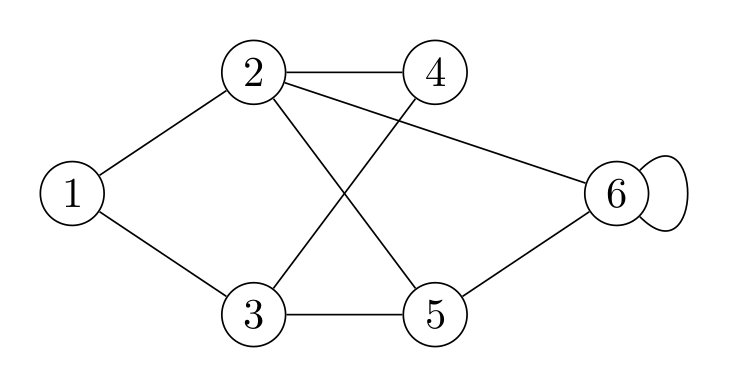
Now the elements of this type of matroid, called graphic matroid, are the edges of the graph (that is, by the way, the reason why I always use $E$ for the ground set of matroids). The feasible collections (i.e. subsets) of $E$ are precisely those that do not include a cycle in the graph. As you can see in the figure, there is an edge that has both its ends at the same vertex (a loop), hence this edge can never be part of a feasible set as it already forms a cycle all by itself. You also notice that for example the four edges along the vertices $1, 2, 4, 3$ form a cycle, thus, we can pick at most three of them.

Now it is time to formally define what a matroid is.

Definition. A pair $M = (E, \mathcal{I})$ on a finite ground set $E$ and $\mathcal{I} \subseteq 2^E$ is a matroid if the following three properties hold

• (I1) $\varnothing \in \mathcal{I}$,
• (I2) if $I \subseteq I’$ and $I’ \in \mathcal{I}$, then $I \in \mathcal{I}$, and
• (I3) if $I, I’ \in \mathcal{I}$ and $|I| < |I’|$, then there exists an $e \in I’ \setminus I$ such that $I + e \in \mathcal{I}$.

This set of rules are called the independence axioms for matroids. The set $\mathcal{I}$ that has to satisfy these axioms contains all the sets that we call independent (previously I refered to them as feasible sets which is in practice often what those sets represent in e.g. optimization problems). Axiom (I1) guarantees that there is at least one independent set, axiom (I2) is the hereditary property that says whenever I take less from an independent set, I stay independent, and axiom (I3) is called the exchange axiom, that says that whenever I start with an independent set $I_1$ and there is another independent set $I_2$ that is larger, then there exists an element in $I_2$ that I can still add to $I_1$ and stay independent. A set that is not independent is called dependent. A set that is dependent but every proper subset is independent is called a circuit, which is motivated by the intuition from graphic matroids: Every set $C$ that is exactly a cycle (and not just contains one) becomes independent by removing any edge.

Let’s briefly check why graphic matroids are in fact matroids. As mentioned above, the independent sets in the graphic matroids are those sets of edges that do not contain a cycle (sometimes these sets are also called forests), so we may write in a bit sloppy fashion $\mathcal{I} = \{F \subseteq E \mid F \text{ is a forest}\}$. Of course (I1) holds as the empty set by definition does not contain anything, including cycles of a graph. Axiom (I2) is also not too hard to believe: If we have a set that does not contain a cycle, we certainly do not obtain one by further removing edges from that set. Axiom (I3) is a bit more complicated to argue: If we consider two forests $F_1, F_2$ in a graph, where $F_2$ contains at least one more edge than $F_1$, then the graph restricted to edges of $F_2$ must have less connected components than the one restricted to $F_1$ (in a forest, each edge reduces the number of connected components by $1$). But this means there must be an edge $e \in F_2$ that connects two of the connected components formed by $F_1$, so this edge is a suitable choice to augment $F_1$.

One might ask how large an independent set can be for a given matroid. The maximal independent sets of matroids are called bases and by the axiom (I3) it is easy to see that every base must have the same cardinality. The size of any base is also called the rank of the matroid.

Now wait a minute, independent sets, bases and ranks? That sounds familiar from linear algebra. In fact these terms are motivated from name twins in vector spaces and matrices (the latter give also an idea from what the name matroid is derived). As it happens, a matrix also does define a matroid (the linear matroid or vector matroid). One might say a matrix is just a set of vectors and for any subset of those vectors we may say that they are independent (in the matroid sense) iff they are linearly independent. Similarly, we can define terms like the span (linear hull), hyperplanes, and few more things, which I will definitely get into in a later blog post.

However, let’s once go back to the example in the beginning. I mentioned a matroid where the only condition for a set to be independent was whether the set is not too large. These kind of matroids are certainly the easiest to think of and they are called uniform matroids which are denoted by $U_n^r$, where $n$ is the size of the ground set $E$ and $r$ is the rank, i.e. a uniform matroid can be uniquely determined (up to isomorphism) by two numbers. To check whether a set $X$ is independent one only needs to count the number of elements in $X$ and check whether this number is not larger than $r$. It is quite easy to check that uniform matroids are in fact matroids.